Тригонометрия – это мощный инструмент в математике! Она изучает связи между углами и сторонами треугольников.
Тригонометрические формулы – это ключи к решению множества задач.
Они позволяют вычислять значения функций, упрощать выражения и доказывать тождества. Разберитесь в них, и мир углов станет понятнее!
Основные тригонометрические функции и их значения для ключевых углов
Давайте разберемся с основными тригонометрическими функциями и их значениями для наиболее часто встречающихся углов. Это фундамент, на котором строится вся тригонометрия! Знание этих значений позволит вам быстро решать многие задачи, не прибегая к калькулятору.
- Синус (sin): Отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
- Косинус (cos): Отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.
- Тангенс (tan): Отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике. Или, что эквивалентно, sin(x) / cos(x).
- Котангенс (cot): Отношение прилежащего катета к противолежащему катету в прямоугольном треугольнике. Или, что эквивалентно, cos(x) / sin(x) или 1 / tan(x).
Ключевые углы, значения тригонометрических функций которых необходимо знать:
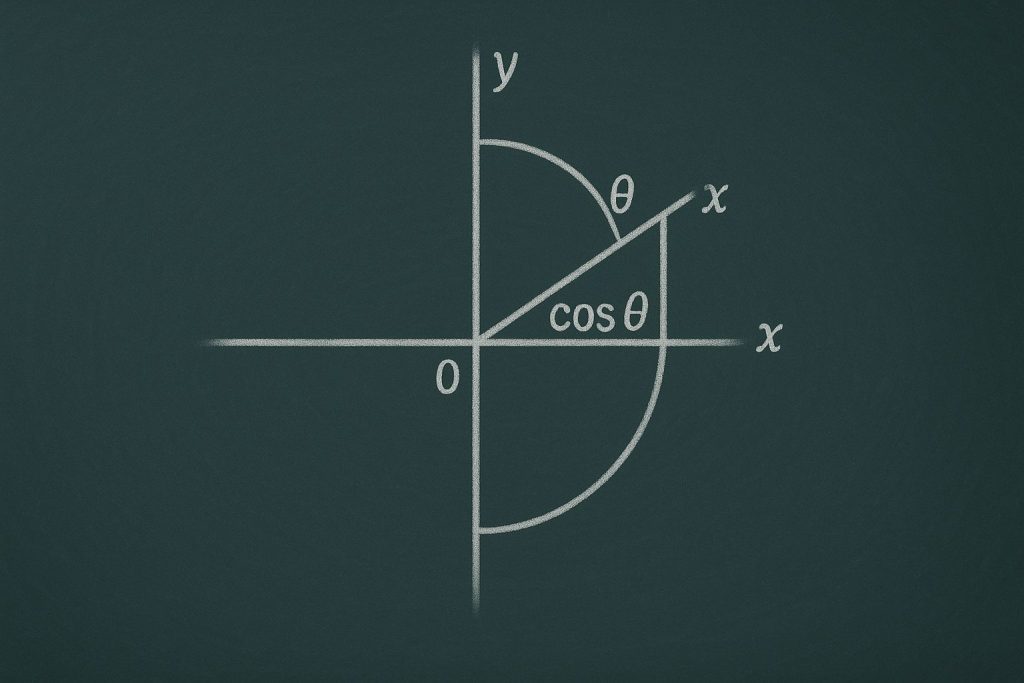
- 0° (0 радиан): sin(0°) = 0, cos(0°) = 1, tan(0°) = 0, cot(0°) ⏤ не определен.
- 30° (π/6 радиан): sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = 1/√3, cot(30°) = √3.
- 45° (π/4 радиан): sin(45°) = √2/2, cos(45°) = √2/2, tan(45°) = 1, cot(45°) = 1.
- 60° (π/3 радиан): sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3, cot(60°) = 1/√3.
- 90° (π/2 радиан): sin(90°) = 1, cos(90°) = 0, tan(90°) ─ не определен, cot(90°) = 0.
Советы по запоминанию:
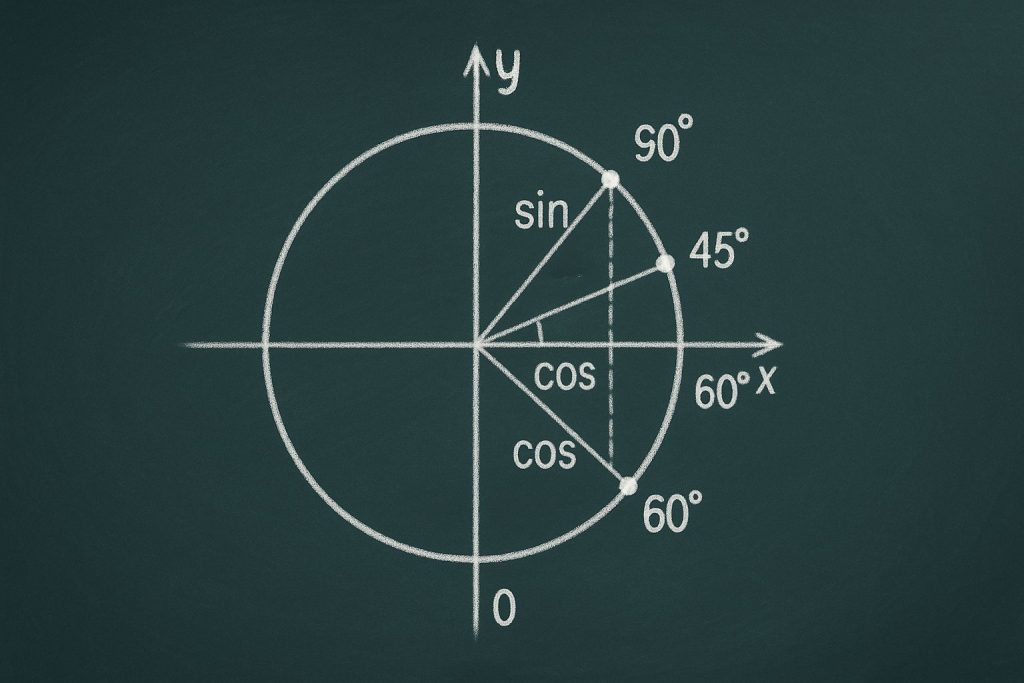
- Круг: Представьте единичную окружность. Синус – это координата y, косинус – координата x.
- Треугольники: Помните про «египетский» треугольник (30-60-90) и равнобедренный прямоугольный треугольник (45-45-90).
- Связи: Тангенс и котангенс легко выводятся из синуса и косинуса.
- Практика: Решайте задачи! Чем больше вы практикуетесь, тем лучше запоминаете.
Понимание этих основных значений и связей между тригонометрическими функциями значительно упростит решение более сложных задач в тригонометрии. Удачи в изучении!
Таблица основных тригонометрических тождеств
Тригонометрические тождества – это равенства, которые остаются верными для всех допустимых значений углов. Они играют ключевую роль в упрощении тригонометрических выражений, решении уравнений и доказательстве других тождеств. Запомнить все тождества сразу может быть сложно, но понимание их происхождения и взаимосвязи значительно упростит задачу.
Вот таблица основных тригонометрических тождеств:
- Основное тригонометрическое тождество: sin²(x) + cos²(x) = 1
- Связь между тангенсом и котангенсом: tan(x) * cot(x) = 1
- Тангенс через синус и косинус: tan(x) = sin(x) / cos(x)
- Котангенс через синус и косинус: cot(x) = cos(x) / sin(x)
- Связь между тангенсом и секансом: 1 + tan²(x) = sec²(x), где sec(x) = 1 / cos(x)
- Связь между котангенсом и косекансом: 1 + cot²(x) = csc²(x), где csc(x) = 1 / sin(x)
Тождества четности/нечетности:
- sin(-x) = -sin(x) (синус – нечетная функция)
- cos(-x) = cos(x) (косинус – четная функция)
- tan(-x) = -tan(x) (тангенс – нечетная функция)
- cot(-x) = -cot(x) (котангенс – нечетная функция)
Пифагоровы тождества (следствия основного тождества):
- sin²(x) = 1 ⏤ cos²(x)
- cos²(x) = 1 ─ sin²(x)
Советы по запоминанию:
- Основное тождество – основа: Все остальные тождества можно вывести из основного (sin²(x) + cos²(x) = 1) и определений тригонометрических функций.
- Визуализация: Представляйте единичную окружность и взаимосвязи между функциями.
- Практика: Решайте задачи на упрощение выражений и доказательство тождеств.
- Группировка: Разделите тождества на группы (основные, четность/нечетность, Пифагоровы) для лучшего запоминания.
Помните, что понимание логики и взаимосвязи между тождествами гораздо важнее, чем механическое заучивание. Используйте эту таблицу как отправную точку, и с практикой вы освоите эти важные инструменты тригонометрии!
Формулы сложения, двойного угла и приведения
Данные формулы играют важную роль в тригонометрии, позволяя выражать тригонометрические функции сложных аргументов через функции более простых углов. Они незаменимы при решении уравнений, упрощении выражений и доказательстве тождеств.
Формулы сложения:
- sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
- sin(α ⏤ β) = sin(α)cos(β) ⏤ cos(α)sin(β)
- cos(α + β) = cos(α)cos(β) ─ sin(α)sin(β)
- cos(α ⏤ β) = cos(α)cos(β) + sin(α)sin(β)
- tan(α + β) = (tan(α) + tan(β)) / (1 ─ tan(α)tan(β))
- tan(α ─ β) = (tan(α) ─ tan(β)) / (1 + tan(α)tan(β))
Формулы двойного угла: (являются частным случаем формул сложения, когда α = β)
- sin(2α) = 2sin(α)cos(α)
- cos(2α) = cos²(α) ⏤ sin²(α) = 2cos²(α) ─ 1 = 1 ⏤ 2sin²(α)
- tan(2α) = 2tan(α) / (1 ⏤ tan²(α))
Формулы приведения: Позволяют выражать тригонометрические функции углов, отличающихся от 0, π/2, π, 3π/2, 2π на угол α, через тригонометрические функции угла α. Общее правило: Определите знак исходной функции в заданной четверти. Если угол представлен как (π/2 ± α) или (3π/2 ± α), то функция меняется на «ко-функцию» (sin на cos, cos на sin, tan на cot и наоборот). Если угол представлен как (π ± α) или (2π ± α), то функция не меняется.
Примеры:
- sin(π/2 + α) = cos(α)
- cos(π ─ α) = -cos(α)
- tan(π + α) = tan(α)
Советы по запоминанию:
- Понимание вывода: Попробуйте вывести формулы сложения из геометрических соображений.
- Ассоциации: Используйте мнемонические правила (например, для синуса «плюс на плюс, минус на минус»).
- Практика: Регулярно решайте задачи, применяя эти формулы.
- Разбиение на части: Разбейте формулы на более мелкие компоненты для лучшего усвоения.
- Единичная окружность: Используйте единичную окружность для визуализации и понимания формул приведения.
Освоив эти формулы, вы значительно расширите свои возможности в решении тригонометрических задач и анализе различных математических моделей.
Примеры решения задач с использованием тригонометрических формул
В этом разделе мы рассмотрим несколько примеров решения задач, демонстрирующих применение изученных тригонометрических формул. Помните, что ключ к успеху – это понимание формул и умение их правильно применять в конкретных ситуациях.
Пример 1: Упрощение тригонометрического выражения.
Задача: Упростите выражение: sin(2x) / (1 + cos(2x))
Решение: Используем формулы двойного угла: sin(2x) = 2sin(x)cos(x) и cos(2x) = 2cos²(x) ⏤ 1. Подставляем в исходное выражение: (2sin(x)cos(x)) / (1 + 2cos²(x) ─ 1) = (2sin(x)cos(x)) / (2cos²(x)) = sin(x) / cos(x) = tan(x)
Ответ: tan(x)
Пример 2: Вычисление значения тригонометрической функции.
Задача: Найдите sin(75°), используя формулы сложения.
Решение: Представим 75° как сумму двух известных углов: 75° = 45° + 30°. Используем формулу сложения для синуса: sin(75°) = sin(45° + 30°) = sin(45°)cos(30°) + cos(45°)sin(30°) = (√2/2)(√3/2) + (√2/2)(1/2) = (√6 + √2) / 4
Ответ: (√6 + √2) / 4
Пример 3: Решение тригонометрического уравнения.
Задача: Решите уравнение: cos(2x) + 3sin(x) = 2
Решение: Используем формулу двойного угла: cos(2x) = 1 ─ 2sin²(x). Подставляем в уравнение: 1 ─ 2sin²(x) + 3sin(x) = 2. Переносим все члены в одну сторону: 2sin²(x) ─ 3sin(x) + 1 = 0. Делаем замену: t = sin(x). Получаем квадратное уравнение: 2t² ─ 3t + 1 = 0. Решаем квадратное уравнение: t = 1 или t = 1/2. Возвращаемся к замене: sin(x) = 1 или sin(x) = 1/2. Решаем каждое уравнение: x = π/2 + 2πk или x = π/6 + 2πk, x = 5π/6 + 2πk, где k – целое число.
Ответ: x = π/2 + 2πk, x = π/6 + 2πk, x = 5π/6 + 2πk, k ∈ Z
Пример 4: Доказательство тригонометрического тождества.
Задача: Докажите тождество: (1 ─ cos(2x)) / sin(2x) = tan(x)
Решение: Используем формулы двойного угла: cos(2x) = 1 ─ 2sin²(x) и sin(2x) = 2sin(x)cos(x). Подставляем в левую часть тождества: (1 ─ (1 ⏤ 2sin²(x))) / (2sin(x)cos(x)) = (2sin²(x)) / (2sin(x)cos(x)) = sin(x) / cos(x) = tan(x). Получили правую часть тождества. Тождество доказано.
Эти примеры демонстрируют, как тригонометрические формулы могут быть использованы для решения разнообразных задач. Практикуйтесь, и вы сможете уверенно применять их в любых ситуациях!



